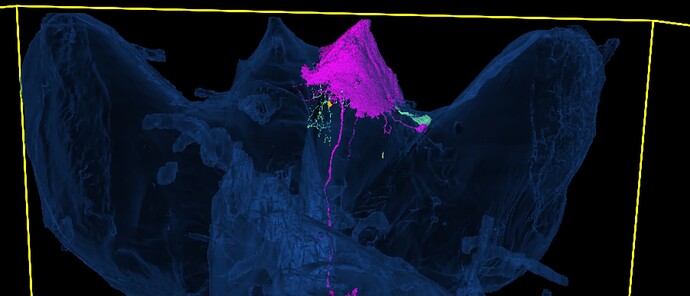
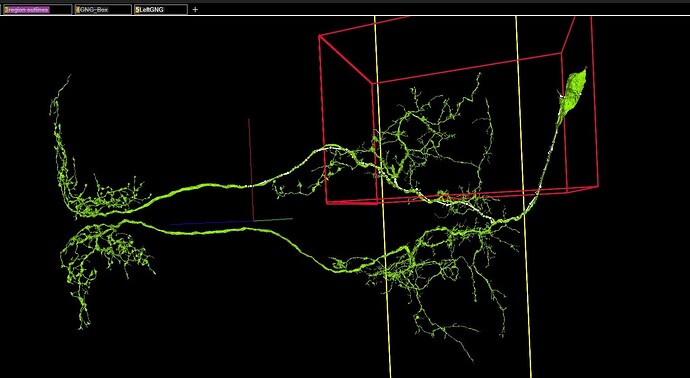
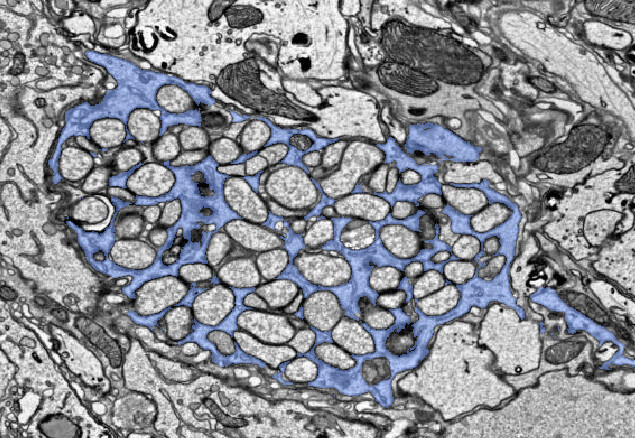
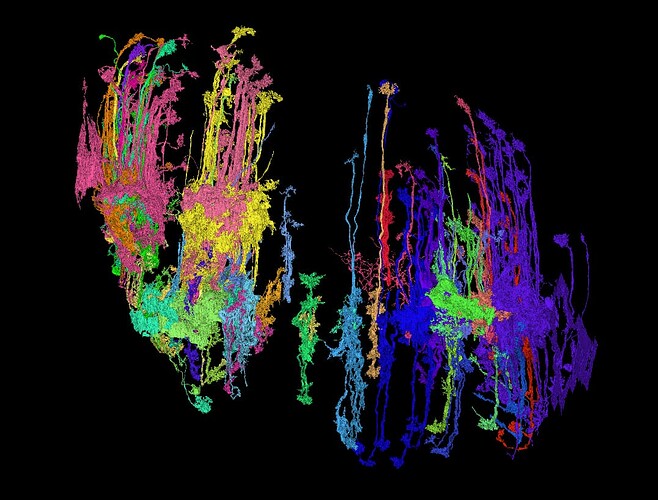
Who are this figure trying to scare
5 Likes
what is that? Ginormous merger?
Yup! There are a few huge carpet mergers that are “unsplittable” in the BANC 
They are working on the backend to hopefully give those areas segmentation so that we can split them apart 
Also, @annkri maybe it’s a ghost trying to protect the treasure trove of scientific knowledge in the BANC 
2 Likes
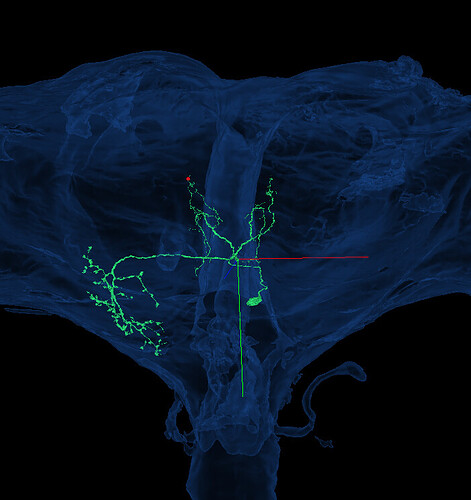
Found the symetrical one :
It is really symetrically created. It’s georgous and soooo mind scaring how nature is capable to do this kinda thing at this scale 
3 Likes
Huge bouton maybe?
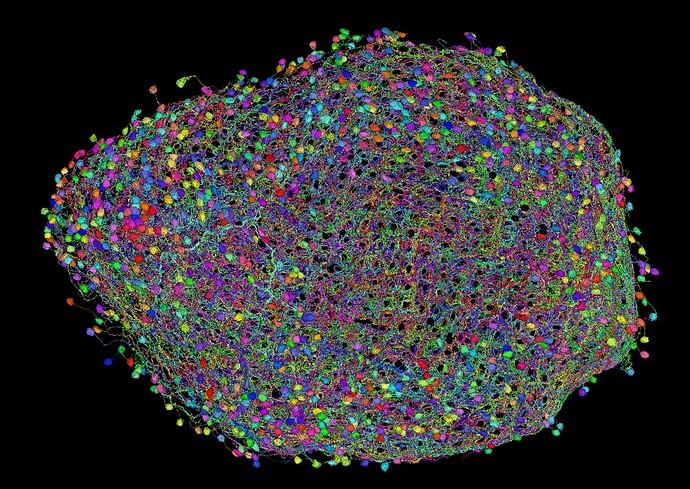
Those are about all the Dm3 cells in the right optic lobe (currently in somewhat rough shape, need some clearing and completing). I like, how you can clearly see the Medulla columns between them (also slightly trypophobic xD).
3 Likes
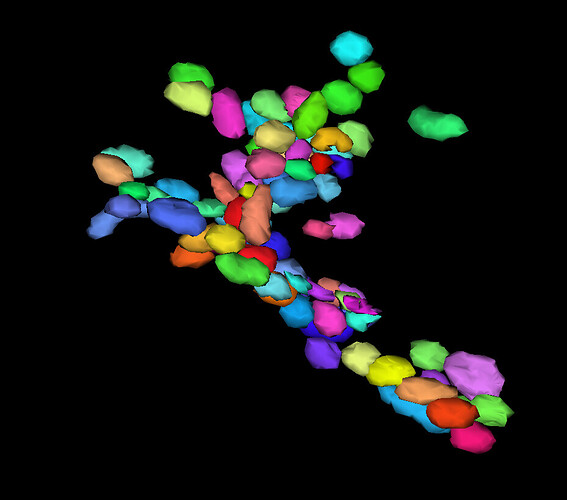
My collection of marbles 
(no idea, what they are)
https://spelunker.cave-explorer.org/#!middleauth+https://global.daf-apis.com/nglstate/api/v1/4966231187652608
3 Likes
https://spelunker.cave-explorer.org/#!middleauth+https://global.daf-apis.com/nglstate/api/v1/4595700372340736
I’m working on a Python script to filter cells against any fiven plane(s).
After a few months of intermittent searching for the solution I was finally able to find one: for each segment ID you can get its leaves (also known as L2 chunks) and then there’s an API to get centroids for each of the leaves. The centroids won’t give you the exact boundaries of a neuron but for my needs it should be more than enough.
The “fun” started, when I wanted to check, if all the centroids lie on the same side of a cutting plane or not. The math is relatively simple, but the scaling between voxels and nanometers took me a whole day to figure out. To be precise, the scaling is simple - [4, 4, 45], but figuring out, that it was the issue for my problems, not so xD. 3 AIs and a day later, I was finally able to solve the issue xD.
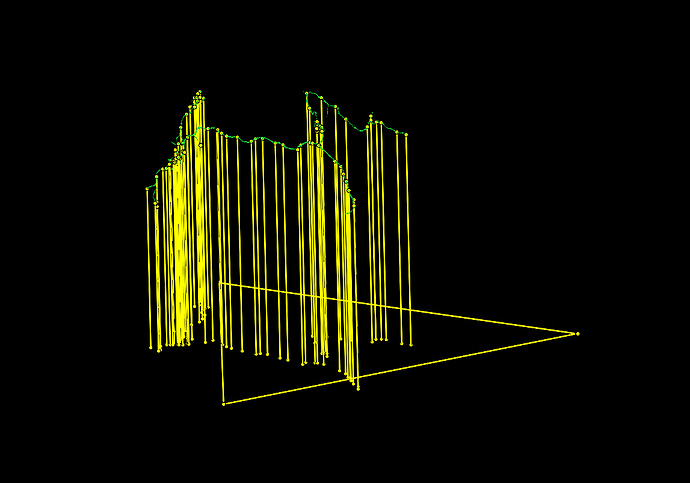
The image shows the cutting plane (the triangle lies on that plane), the centroids (yellow points on the surface of the green neuron) and sections showing the distances between each of the centroids and the plane. The math is that if the length is positive the points lies on one side of the plane, if negative (negative lengths, lol), the point is on the other.
Fortunately, the one above is correct, but I also had results like the one below xD
https://spelunker.cave-explorer.org/#!middleauth+https://global.daf-apis.com/nglstate/api/v1/5597585380212736
2 Likes